Predictions & Data for this entry
| Model: stx | climate: BSk, Csa, Cfb, Dfb | migrate: | phylum: |
| COMPLETE = 2.9 | ecozone: THp, TA | food: bxM, xiH | class: |
| MRE = 0.042 | habitat: 0iTg, 0iTs | gender: Dg | order: |
| SMSE = 0.009 | embryo: Tv | reprod: O | family: |
Zero-variate data
| Data | Observed | Predicted | (RE) | Unit | Description | Reference |
|---|---|---|---|---|---|---|
| tg | 31.5 | 37.89 | (0.203) | d | gestation time | FootCarn2000 |
| tx | 35 | 35.07 | (0.002136) | d | time since birth at weaning | FootCarn2000 |
| tp | 168 | 93.24 | (0.445) | d | time since birth at puberty - females | FootCarn2000 |
| tp2 | 91 | 93.24 | (0.02467) | d | time since birth at puberty - females (youngest females in exp) | BayeXXXX |
| tp_m | 140 | 141 | (0.006821) | d | time since birth at puberty - males | FootCarn2000 |
| am | 3285 | 3658 | (0.1137) | d | life span | AnAge |
| Lb | 8 | 12.14 | (0.5174) | cm | kit crown-rump length | ResearchGate |
| Li | 50 | 41.53 | (0.1695) | cm | ultimate crown-rump length | wiki |
| Wwb | 53.57 | 39.2 | (0.2682) | g | wet weight at birth - New Zealand | FootCarn2000, FadaFato2018, AporHaga2014 |
| Wwp | 2720 | 2597 | (0.04509) | g | wet weight at puberty - New Zealand - females | BayeXXXX |
| Wwi | 5000 | 5173 | (0.03454) | g | ultimate wet weight - females | FootCarn2000 |
| Wwi_m | 5500 | 5301 | (0.03621) | g | ultimate wet weight - males | FootCarn2000 |
| Ri | 0.08904 | 0.1416 | (0.5899) | #/d | maximum reprod rate | HolsHutz2002 |
Uni- and bivariate data
| Data | Figure | Independent variable | Dependent variable | (RE) | Reference |
|---|---|---|---|---|---|
| tWw_1 |   | time since birth | wet weight | (0.2128) | BergChaz1976 |
| tWw_2 |   | time since birth | wet weight | (0.03207) | MasoShap1986 |
| tWw_3 |   | time since birth | wet weight | (0.03413) | MasoShap1986 |
| tL | 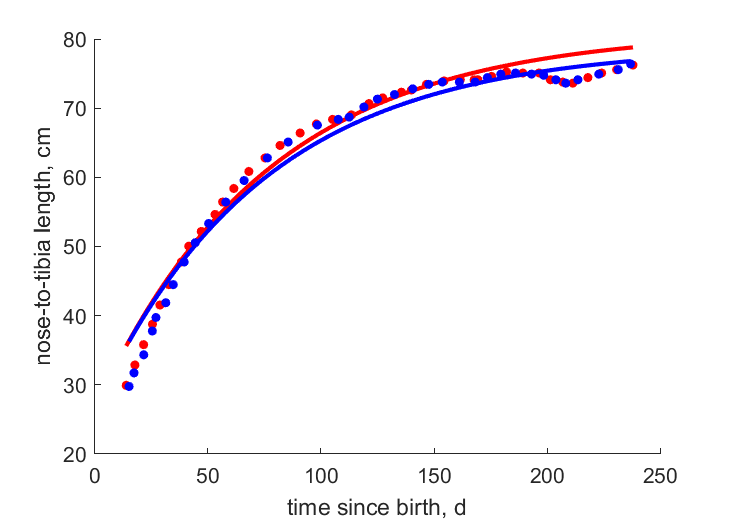  | time since birth | nose-to-tibia length | (0.02863) | MasoShap1986 |
| tL2 |   | time since birth | nose-to-tibia length | (0.02981) | MasoShap1986 |
| tWw_4 | 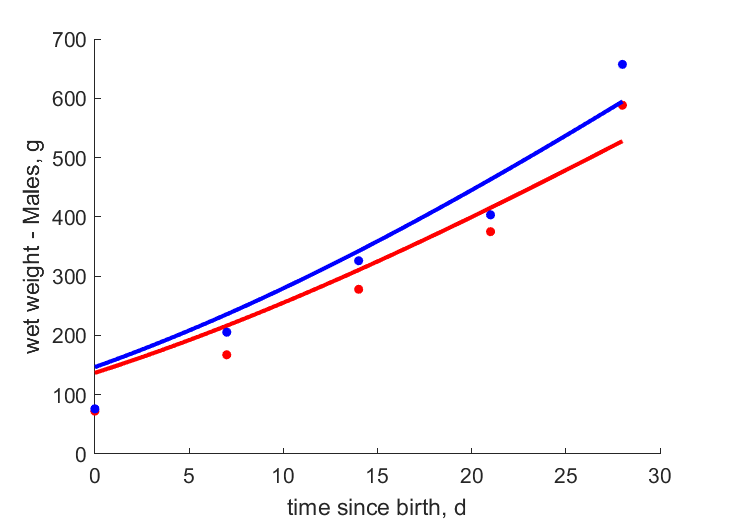  | time since birth | wet weight - Males | (0.1667) | Mahm2013 |
| tWw_5 |   | time since birth | wet weight - Males | (0.1437) | Mahm2013 |
| tWw_6 | 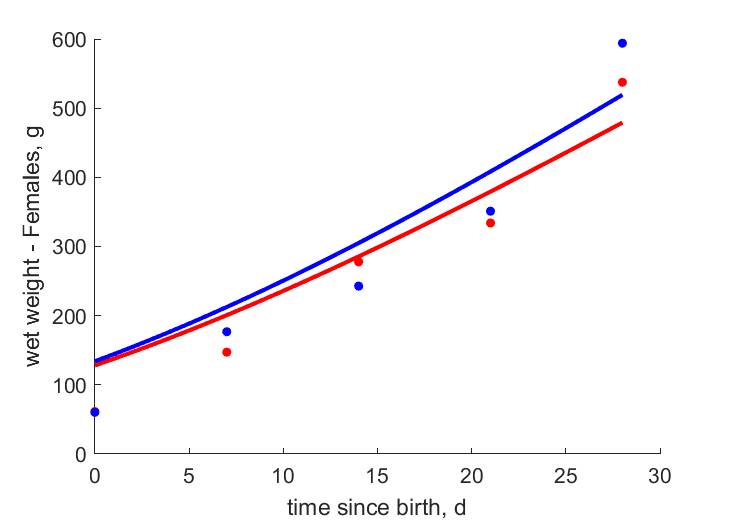  | time since birth | wet weight - Females | (0.1707) | Mahm2013 |
| tWw_7 |   | time since birth | wet weight - Females | (0.2134) | Mahm2013 |
| tWw_0154 | 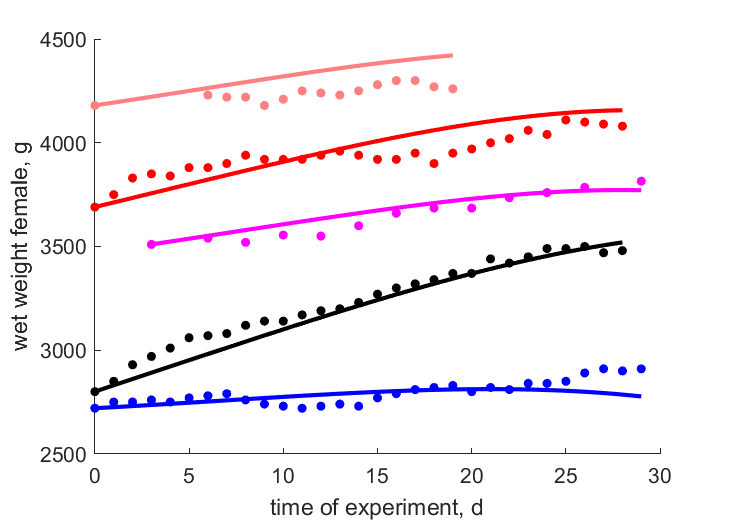  | time of experiment | wet weight female | (0.02278) | Baye1999a |
| tWw_0192 |   | time of experiment | wet weight female | (0.01718) | Baye1995 |
| tWw_1085 |   | time of experiment | wet weight female | (0.009174) | Baye2003 |
| tWw_0397 |   | time of experiment | wet weight female | (0.01346) | Baye1999b |
| tWw_0203 |   | time of experiment | wet weight female | (0.01229) | Baye1988 |
| tJX_0154 | 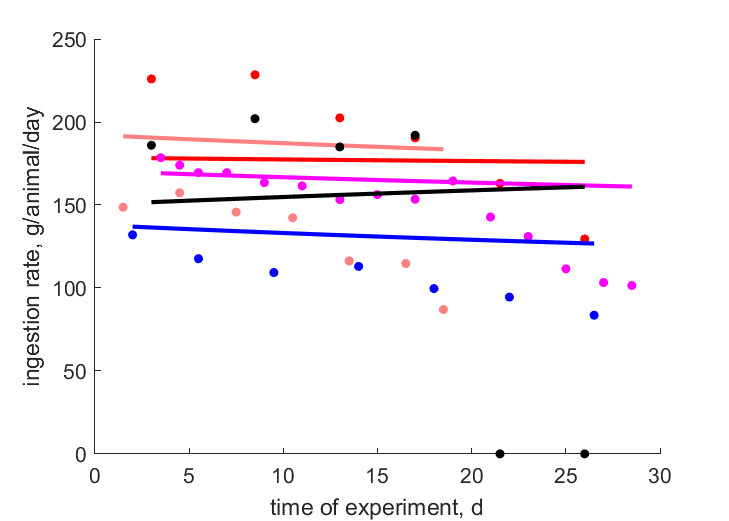  | time of experiment | ingestion rate | (0.4369) | Baye1999a |
| tJX_0192 |   | time of experiment | ingestion rate | (0.1733) | Baye1995 |
| tJX_1085 |   | time of experiment | ingestion rate | (0.125) | Baye2003 |
| tJX_0397 |   | time of experiment | ingestion rate | (0.2295) | Baye1999b |
| tJX_0203 |   | time of experiment | ingestion rate | (0.6089) | Baye1988 |
| WwN_0154 | 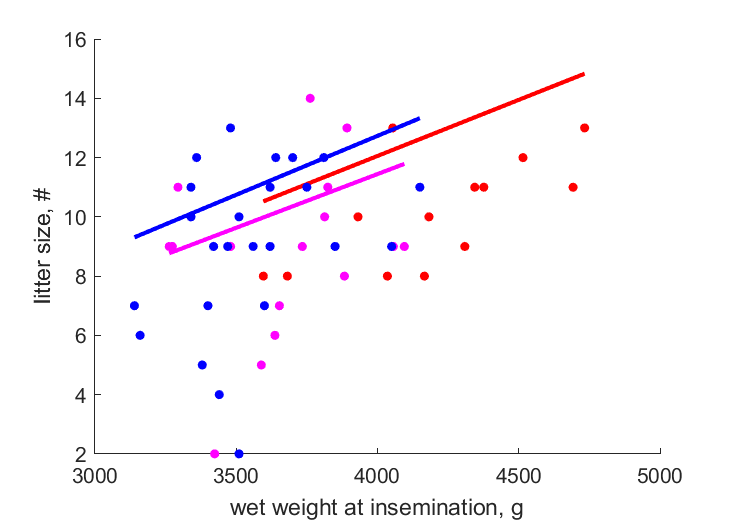  | wet weight at insemination | litter size | (0.2734) | Baye1999a |
| WwN_0192 |   | wet weight at insemination | litter size | (0.2764) | Baye1995 |
| WwN_1085 |   | wet weight at insemination | litter size | (0.2694) | Baye2003 |
| tW_e2 |   | age | wet weight of foetus | (0.2352) | ZaikDom2013 |
| tWwe_Baye |   | age | wet weight of foetus | (0.149) | BayeXXXX |
Pseudo-data at Tref = 20°C
| Data | Generalised animal | Oryctolagus cuniculus NZW | Unit | Description |
|---|---|---|---|---|
| v | 0.02 | 0.03803 | cm/d | energy conductance |
| kap | 0.8 | 0.7846 | - | allocation fraction to soma |
| kap_R | 0.95 | 0.95 | - | reproduction efficiency |
| p_M | 18 | 1576 | J/d.cm^3 | vol-spec som maint |
| k_J | 0.002 | 0.002 | 1/d | maturity maint rate coefficient |
| kap_G | 0.8 | 0.8016 | - | growth efficiency |
| t_0 | 0 | 1.326e-06 | d | time at start development |
Discussion
- Males are assumed to differ from females by {p_Am} and E_Hp only
- Different to version : Added data on pregnant females, and dget_EVH_AF to derive their dynamics. We assumed no saturating function of litter size (Seff = del_upreg). For an example of saturating function see Wistar rat entry.
- To avoid negative growth (shrinking), a condition dV = max( 0,pG/E_G ) in inserted in get_EVH_AF;
- Rabbit entry needs a bit more work and adjustment of the equations relating to pregnancy, as well as to feeding because coprophagia(eating of foeces) should perhaps be explicitly modelled if ingestion data are of interest. For foetal development, more data on foetal length and weight is needed, as it is currently impossible to know whether a constant body composition is maintained throughout foetaldevelopment (resulting in constant reserve density) or reserve density fluctuates depending on the condition of the mother or number of siblings in a litter.
- Parameter estimation is slow due to the code complexity; with more continuations a different parameter set might be obtained.
Acknowledgment
- This entry (version 2019/12/12) was financially supported by Bayer.
Bibliography