Parameter-values are individual-specific, but intra-specific differences between individuals are small relative to inter-specific ones.
So it remains meaningfull to talk about species-specific parameters values as means of those of individuals of that species.
Once we know the parameters, we can compute many properties (traits), even if these properties have not been measured.
DEB theory has implied rules for the covariation of parameters, based on plain physics, but ecological and evolutionary adaptation can modify these rules.
Quite a few papers have been written on the various patterns in DEB parameters and derived traits;
the Supporting Information for these papers shows how to extract these patterns from the AmP collection,
see
DEB papers.
Clicking on the markers in the resulting plots shows the name of the corresponding species.
Click here for a poster that summerizes the five patterns in parameter values that have been identified so far.
This page shows some examples of relationships between traits.
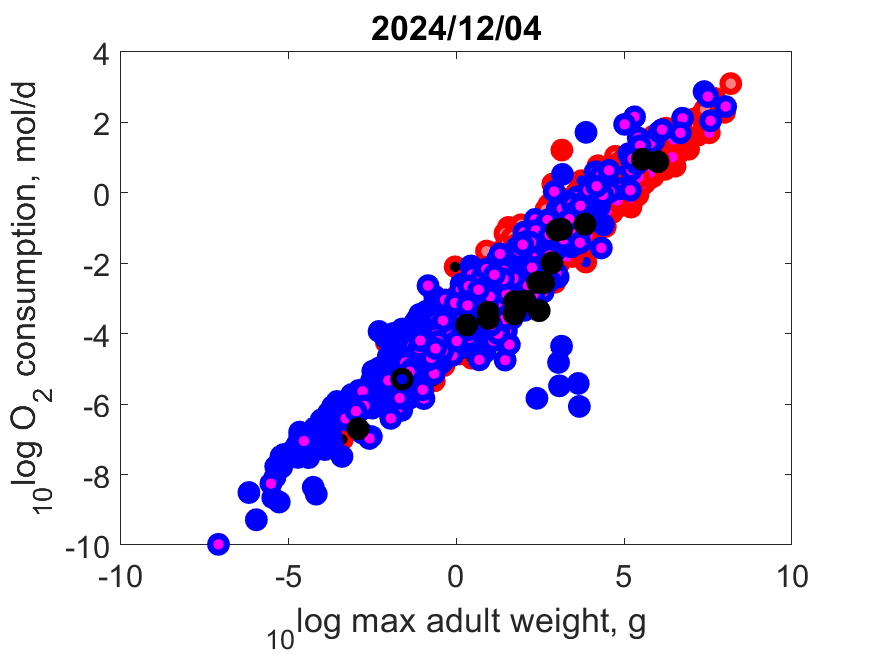
Left: Log dioxygen consumption as function of log maximum adult body weight at T
ref.
Dioxygen consumption has a number of adding contributions,
such as from digestion, growth and reproduction overheads (or maturation in pre-adults) and maturity and somatic maintenance.
DEB theory has no assumptions about respiration and gets it by closing the mass balance for chemical elements (C, H, O and N).
In this way it respects the additive nature of contributions to respiration.
The reason why respiration of fully grown adults is less than proportional to mass is because reserve density tends to increase with maximum weight,
see
Kooy1986,
while reserve does not require maintenance, and because small-bodied species are more frequently in a hurry,
see
Kooy2013.
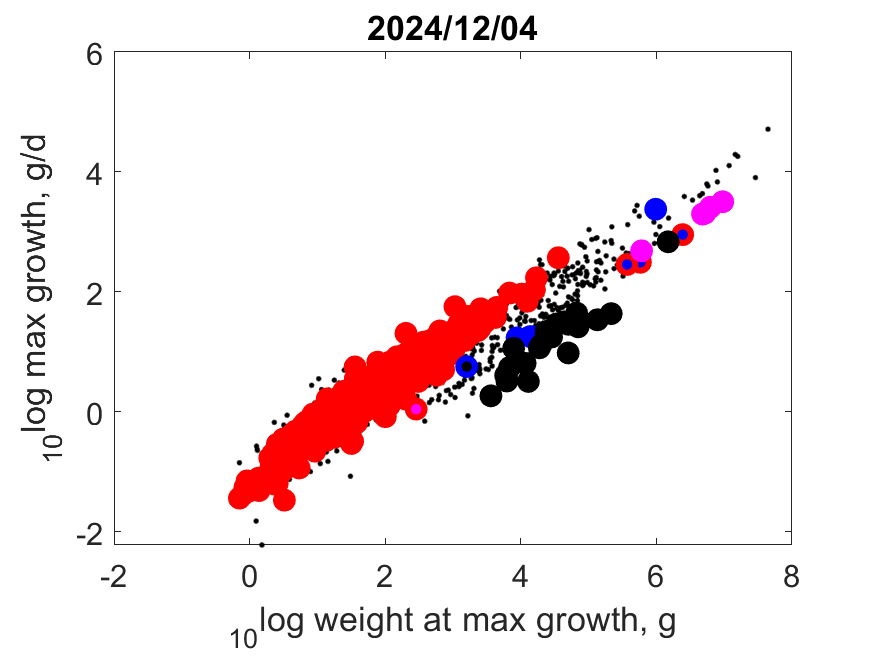
Right: Log maximum growth as function of log (wet) weight at maximum growth at Tref.
Contrary to popular belief, the big dinosaurs did not grow exceptionally fast, given their body mass.
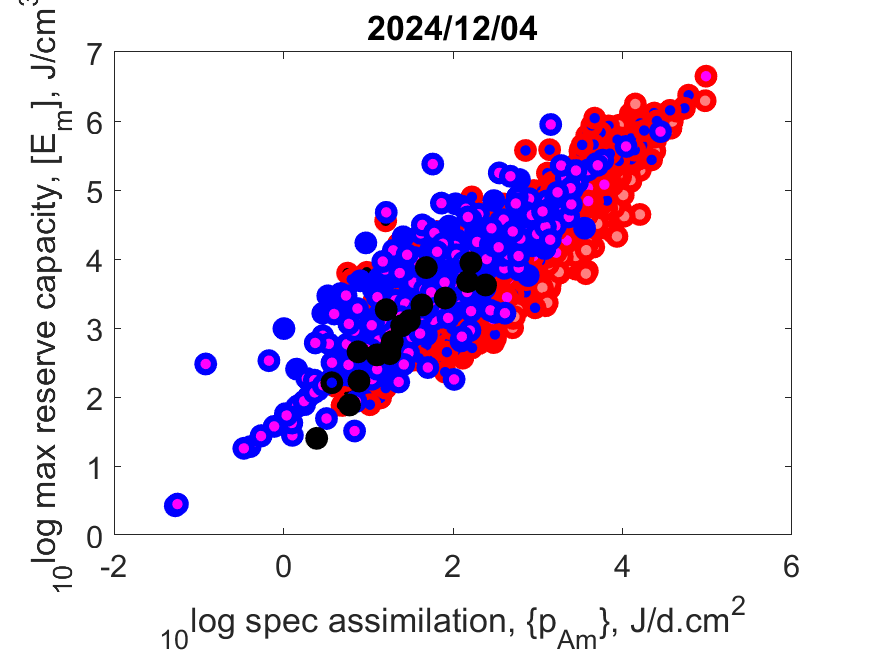
Left: Log reserve capacity [E
m] as function of log specific assimilation rate {p
Am} at T
ref.
This capacity is the ratio of the surface-area-specific assimilation rate and the energy conductance, i.e. input to and output from reserve,
while the latter does not vary that much.
Since large-bodied species have a larger capacity, they can starve for a longer period, also because they have a small specific somatic maintenance.
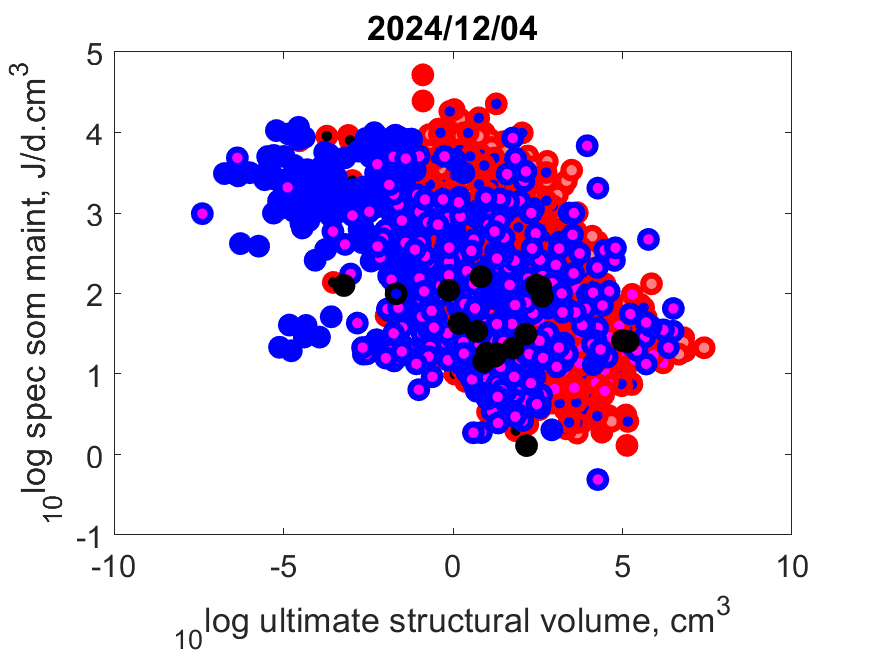
Right: Log volume-specific somatice maintenance [pM] as function of log maximum structural volume Lm3 at Tref.
Small-bodied species more frequently compress their life cycle in a short period and synchronize it with a temporary abundance of their resource.
They need to combine this with a torpor state in periods when resources are scarse, or else migrate or change diet.
Herbivors can only grow fast, for instance, when they manage to squeeze their growth period in that of plants, since only then plants are rich in proteins
that herbivors need for growth.
The plant growth season might be short in some habitats.
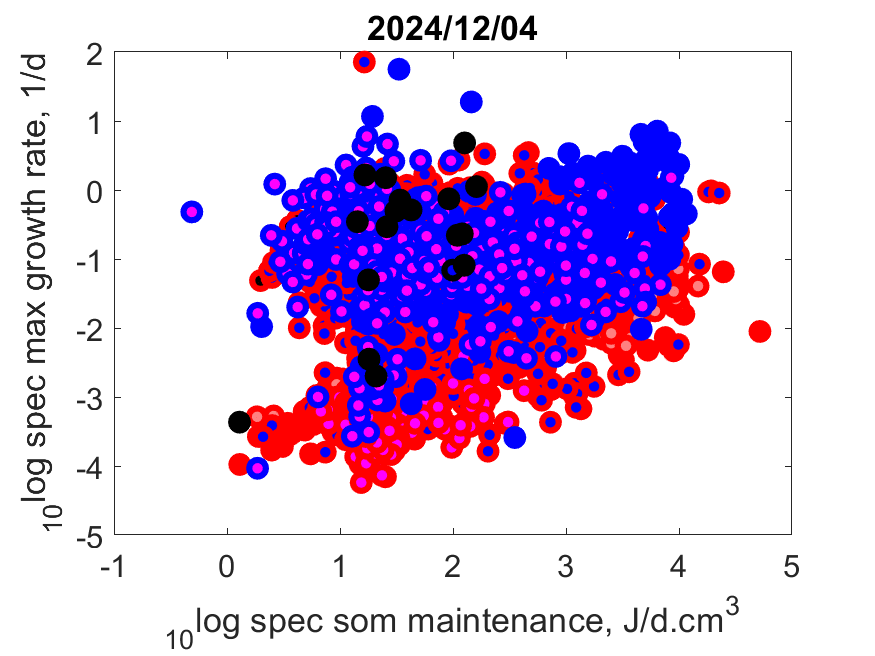
Left: Log specific maximum growth rate r
m as function of log specific somatic maintenance [p
M] at T
ref.
The few with high r
m and relatively low [p
M] are all insects that suddenly cease growing and switch to a next stage.
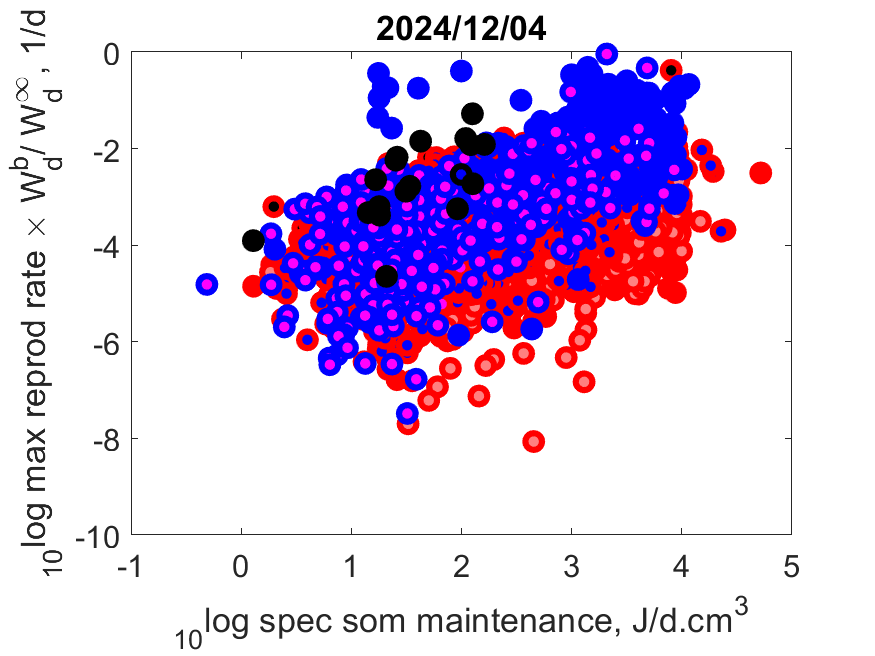
Right: Log of the product of maximum reproduction and dry weight at birth as fraction of ultimate dry weight
RiWdb/Wdi as function of log specific somatic maintenance [pM] at Tref.
These plots for fully-grown invertebrates (left) and vertebrates (right) show
the fraction of mobilised reserve allocated to soma, κ,
the fraction of assimilation allocated to reproduction, κ
RA,
and the supply stress, s
s, i.e. maturity maintenance times the squared somatic one, divided by cubed assimilation.
The latter dimensionless quantity can take values between zero (for supply species) and 4/27 (for demand species).
The mesh is defined by κ
RA = 1 - κ - s
s/ κ
2.
All points are on this mesh, but some invertebrates and some ray-finned fish deviate a little due to metabolic acceleration;
generally s
s remains constant during the life cycle, but decreases during acceleration.
No tetrapod accelerates.
The values that κ can take depend on the supply stress, as indicated in the plots.
The upper boundary is better populated than the lower one.
Only for s
s=0 can κ span the full range between 0 and 1.
Outside this range, puberty cannot be reached, so the life cycle cannot be completed.
Notice that ecdysozoa (especially insects) are masters of the supply strategy, and vertebrates (especially birds and mammals) are masters of the demand strategy.
Many properties of species depend on where they are in the supply-demand spectrum,
see
LikaAugu2014.