A food chain in the chemostat

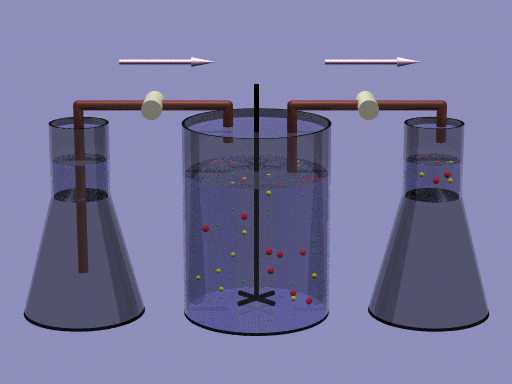Vessels:
Left: supply with substrate
Middle: culture vessel (well stirred)
Right: overflow

Pumps:
Left: supply
Right: removal

Dots: organisms
Arrows: flow direction

A microbial food chain can be studied in a chemostat, where the volume in the culture vessel is kept constant, by puming at constant rates. There are two control parameters: the specific dilution rate of the chemostat, and the concentration of substrate in the supply vessel.

The Monod model of a tri-trophic chain (which is a special case of the DEB model) is described by a system of 4 ordinary differential equations: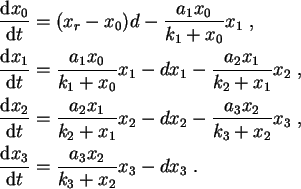

The four variables are:

  • x0: the concentration of substrate
  • xi: the densities of the populations of the i-th trophic level (prey, predator, top-predator)
Parameters:
  • d: the specific dilution rate
  • xr: the substrate concentration in the feed
  • ki: the saturation coefficient for level i
  • ai: the maximum specific feeding rate for level i

First equation: The first term on the right-hand side describes the supply and removal of substrate; the second term represents the ingestion of substrate by the prey-population. Second equation: the three terms correspond with the growth of the prey population, the disappearance of prey by removal and by predation. The expressions for the rates of change of the predators and top-predators have the same form.

Since mass conservation implies that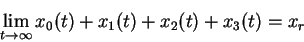

the analysis of the asymptotic behaviour of the four dimensional system can be reduced to the following three dimensional system:


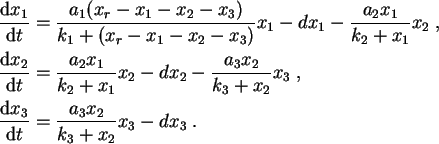
The following parameter values were used in our computations:


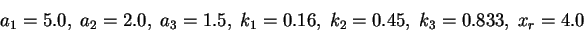
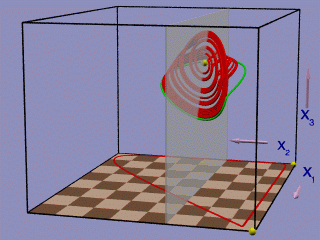
Left figure: dilution rate d = 0.870; no stable coexistence of all trophic levels, there are both heteroclinic and homoclinic orbits to the saddle cycle (the green periodic orbit).

Right figure: dilution rate d = 0.876; a chaotic attractor exists that suddenly disappears at a homoclinic bifurcation of the saddle cycle (the green periodic orbit) if the dilution rate is lowered to d = 0.873.

The transparent plane in both pictures is the nullcline for the top-predator: on this plane the net growth rate of the top-predator population is zero.